✅ 너비 우선 탐색 (BFS, Breadth-First Search)
❕ 기본 개념
- 그래프의 시작점에서 간선(edge)을 따라가며 정점(node)을 탐색하고 지정한 목표 정점에 도달하는 것
- BFS는 그래프의 시작점부터 가까운 순으로 너비를 넓혀 가며 탐색하는 알고리즘
- 따라서 목표가 시작점에 가까이 있으면 탐색이 빨리 종료됨
- 후보 노드를 선입선출(FIFO) 구조로 관리하므로 queue 데이터 구조를 사용
- 따라서 queue와 while loop을 이용하여 BFS를 구현함
❕ 작동 방식

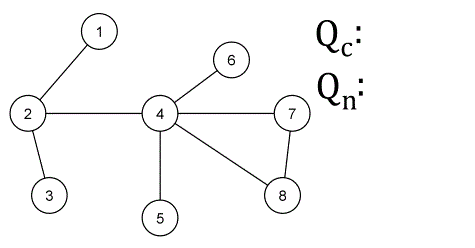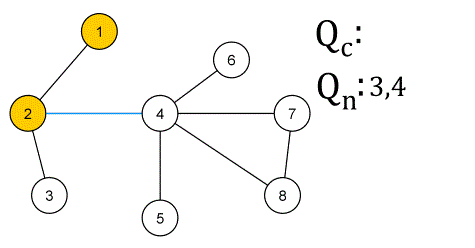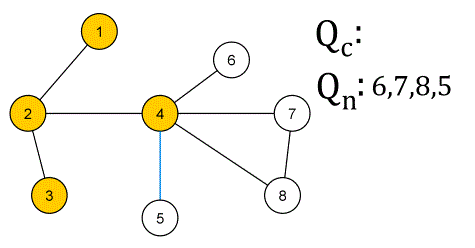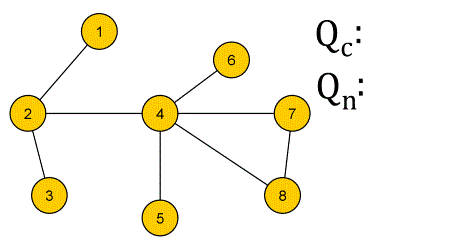
✔ 활용 예시
queue의 특징이 필요한 부분이나 너비를 우선으로 탐색하는 것이 효율적인 곳에 사용됨
ex. 최단거리를 구하는 문제
☞ BFS로 가까운 노드부터 탐색하기 때문에, 가장 먼저 찾아지는 해답이 곧 최단거리가 됨
✔ 구현 방법 (JS)
// DATA
const airports = 'PHX BKK OKC JFK LAX MEX EZE HEL LOS LAP LIM'.split(' ');
const routes = [
['PHX', 'LAX'],
['PHX', 'JFK'],
['JFK', 'OKC'],
['JFK', 'HEL'],
['JFK', 'LOS'],
['MEX', 'LAX'],
['MEX', 'BKK'],
['MEX', 'LIM'],
['MEX', 'EZE'],
['LIM', 'BKK'],
];
// The graph
const adjacencyList = new Map();
// Add node
function addNode(airport) {
adjacencyList.set(airport, []);
}
// Add edge, undirected
function addEdge(origin, destination) {
adjacencyList.get(origin).push(destination);
adjacencyList.get(destination).push(origin);
}
// Create the Graph
airports.forEach(addNode);
routes.forEach(route => addEdge(...route))// BFS
function bfs(start) {
const visited = new Set();
const queue = [start];
while (queue.length > 0) {
const airport = queue.shift(); // mutates the queue
const destinations = adjacencyList.get(airport);
for (const destination of destinations) {
if (destination === 'BKK') {
console.log(`BFS found Bangkok!`)
}
if (!visited.has(destination)) {
visited.add(destination);
queue.push(destination);
}
}
}
}
bfs('PHX')
✅ 깊이 우선 탐색 (DFS, Depth-First Search)
❕ 기본 개념
- BFS와 마찬가지로 시작점으로부터 지정한 정점에 도달하는 것이 목적인 그래프 탐색 알고리즘
- 노드를 탐색할 때 하나의 길을 끝까지 따라가고, 더 이상 진행할 수 없는 곳에 다다르면 다음 후보가 되는 길을 탐색함
- 즉, 깊이 우선 탐색은 하나의 길을 깊이 있게(수직으로) 찾아가는 방식
- 후보 노드를 후입선출(LIFO) 구조로 관리하므로 stack 데이터 구조를 사용
- 따라서 stack과 재귀함수를 이용하여 DFS를 구현함
❕ 작동 방식


✔ 활용 예시
stack의 특징이 필요한 부분이나 깊이를 우선적으로 탐색하는 것이 효율적인 곳에 사용됨
ex. 경로의 특징을 저장해야 하는 문제
✔ 구현 방법 (JS)
// DFS
function dfs(start, visited = new Set()) {
console.log(start)
visited.add(start);
const destinations = adjacencyList.get(start);
for (const destination of destinations) {
if (destination === 'BKK') {
console.log(`DFS found Bangkok`)
return;
}
if (!visited.has(destination)) {
dfs(destination, visited);
}
}
}
dfs('PHX')
✅ BFS vs. DFS

| BFS (너비우선탐색) | DFS (깊이우선탐색) |
| 현재 정점에 연결된 가까운 노드부터 탐색 | 현재 정점에서 끝까지 내려가면서 탐색 |
| queue | stack / recursive function |
| 인접 리스트 : O(N+E) 인접 행렬 : O(N²) |
인접 리스트 : O(N+E) 인접 행렬 : O(N²) |
▶ 시간 복잡도
인접 행렬 - 노드의 개수 N만큼 도는 2중 for문을 돌려 두 노드 사이에 간선(edge)이 존재하는지 확인해야 함
인접 리스트 - 다음 노드를 방문했는지 확인할 때 간선의 개수(E)의 두 배만큼의 시간이 걸리고, 각 노드를 방문할 때 정점의 개수인 N만큼 시간이 걸림. 따라서 O(N+2*E) = O(N+E)가 됨
참고자료
Level-based BFS example, DFS Algorithm, DFS
Graph Traversal with BFS and DFS
'Devlog > DS & Algorithms' 카테고리의 다른 글
| [알고리즘] 삽입 정렬 (0) | 2022.08.05 |
|---|---|
| [알고리즘] 선택 정렬 (0) | 2022.08.05 |
| [알고리즘] 완전탐색기법 (0) | 2022.07.30 |
| [자료구조] Heap (0) | 2022.07.22 |
| [자료구조] Hash Table (0) | 2022.07.16 |